DDPM:一文从理解到公式推导
文章目录
【注意】最后更新于 September 8, 2024,文中内容可能已过时,请谨慎使用。
DDPM ,即 Denoising Diffusion Probabilistic Models。其得益于热力学研究:向一杯水滴入颜料后,无论如何滴入,最终颜料都会均匀分布在水中;而如果我们能预测每一刻颜料的变化状态,那我们就能恢复出颜料滴入的初始状态。在 DDPM 中即是认为逐步向图像中加入噪音(“颜料”),随着加入的步骤增多,最终图像是符合某种稳定分布(正态分布)的。那么只需要通过模型预测出每一步加入的噪音就可以从一个状态分布采样的噪音 \(\mathbf{x}_t\) 逆转为图像 \(\mathbf{x}_0\),如下图所示。
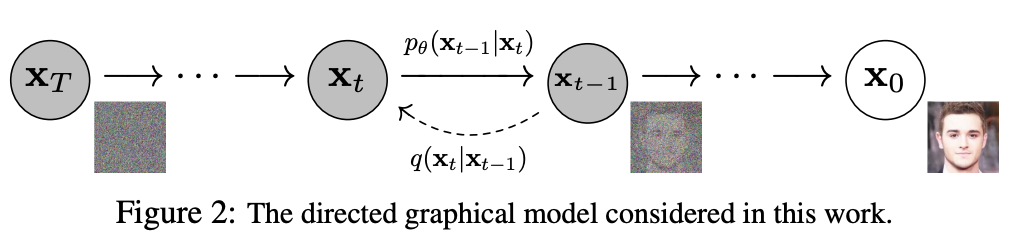
Forward Process
Forward Process 过程即从图像 \(\mathbf{x}_0\) 到噪音 \(\mathbf{x}_t\) 的过程,需要经历 \(t\) 次加噪。在 DDPM 中,其假设每次加入的噪音都是符合正态分布的(均值为 \(\sqrt{1 - \beta_t} x_{t-1}\),方差为 \(\beta_t \mathbf{I}\);这里值得注意的是 \(\beta_t\) 是一个预先定义的序列,是已知的),可以表示为:
\[ q(\mathbf{x}_{t}|\mathbf{x}_{t-1})=\mathcal{N}(\sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}) \]
即代表已知道 \(\mathbf{x}_{t-1}\) 的情况下, \(\mathbf{x}_t\) 服从上述的正态分布,为了更易于理解,这里可以根据上式得出 \(\mathbf{x}_t\) 的表达式:
\[ \mathbf{x}_{t} = \sqrt{1 - \beta_t} \mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} \]
式中 \(\epsilon_{t-1} \sim \mathcal{N}(0, \mathbf{I})\),是一个标准正态分布,\(\beta_t\) 是一个参数,可以理解为扩散速度,其值越大代表加入的噪音越多、保留的原信息越少,在扩散过程中 \(\beta_t\) 不断增加(\(0<\beta_0<\beta_1<...<\beta_T<0\)),因为扩散速度是不断增加的。
而我们在 Forward Process 中只知道 图像 \(\mathbf{x}_0\) ,因此如何通过 \(\mathbf{x}_0\) 来计算任意 \(\mathbf{x}_t\) 呢?我们首先观察上式发现 Forward Process 中任意一个时刻的状态 \(\mathbf{x}_t\) 只依赖于 \(\mathbf{x}_{t-1}\) ,与之前的状态无关,即符合马尔可夫链过程。那么根据链式法则,可以表示为:
\[ q(\mathbf{x}_{1:T} | \mathbf{x}_0) = \prod_{t=1}^T q(\mathbf{x}_t | \mathbf{x}_{t-1}) \]
进一步的,我们可以表达为:
\[ \mathbf{x}_{t} = \sqrt{1 - \beta_t} \mathbf{x}_{t-1} + \sqrt{\beta_t}\epsilon_{t-1} \\ \mathbf{x}_{t-1} = \sqrt{1 - \beta_{t-1}} \mathbf{x}_{t-2} + \sqrt{\beta_{t-1}}\epsilon_{t-2} \]
将其代入可以得到
\[ \begin{align} \mathbf{x}_{t} &= \sqrt{1 - \beta_t} (\sqrt{1 - \beta_{t-1}} \mathbf{x}_{t-2} + \sqrt{\beta_{t-1}}\epsilon_{t-2}) + \sqrt{\beta_t}\epsilon_{t-1} \\ &=\sqrt{(1 - \beta_{t-1})(1 - \beta_{t})} \mathbf{x}_{t-2} + \sqrt{(1 - \beta_t)\beta_{t-1}} \epsilon_{t-2} + \sqrt{\beta_t}\epsilon_{t-1} \end{align} \]
我们可以定义 \(\alpha_t = 1 - \beta_t\),则 \(\bar{\alpha}_t = \prod_{i=1}^{t} \alpha_i =\prod_{i=1}^{t}(1 - \beta_i)\),即可表示为:
\[ \begin{align} \mathbf{x}_{t} &=\sqrt{\alpha_{t-1}\alpha_{t}} \mathbf{x}_{t-2} + \sqrt{\alpha_{t}(1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_{t}}\epsilon_{t-1} \end{align} \]
由正态分布的再生性:如果随机变量 \(X \sim N(\mu_1, \sigma_1^2)\) 和 \(Y \sim \mathcal{N}(\mu_2, \sigma_2^2)\),那么\(aX + bY \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2)\)。我们可以将两次采样变为一次采样,即参数重整化:
\[ \begin{align} \mathbf{x}_{t} &=\sqrt{\alpha_{t-1}\alpha_{t}} \mathbf{x}_{t-2} + \sqrt{\alpha_{t}(1-\alpha_{t-1})+1-\alpha_{t}} \epsilon \\ &=\sqrt{\alpha_{t-1}\alpha_{t}} \cdot\mathbf{x}_{t-2} + \sqrt{1-\alpha_{t-1}\alpha_{t}} \cdot\epsilon \end{align} \]
式中 \(\epsilon \sim \mathcal{N}(0, \mathbf{I})\),以此类推,可以表达为:
\[ \begin{align} \mathbf{x}_t &= \prod_{i=1}^{t} \sqrt{\alpha_i} \cdot \mathbf{x}_0 + \sqrt{1-\prod_{i=1}^{t}\alpha_i} \cdot \epsilon \\ &=\sqrt{\bar \alpha_t} \cdot \mathbf{x}_0 + \sqrt{1-\bar\alpha_t} \cdot \epsilon \end{align} \]
即可以直接表达为:
\[ q(\mathbf{x}_{t}|\mathbf{x}_{0})=\mathcal{N}(\sqrt{\bar \alpha_t} \mathbf{x}_{0}, ({1-\bar \alpha_t})\mathbf{I}) \]
Reverse Process
Reverse Process 即 Forward Process 的反方向, 是从噪音 \(\mathbf{x}_t\) 得到图像 \(\mathbf{x}_0\) 的过程。如 Reverse Process 的公式 \(\mathbf{x}_t =\sqrt{\bar \alpha_t} \cdot \mathbf{x}_0 + \sqrt{1-\bar\alpha_t} \cdot \epsilon\) 可以一步推出:
\[ \mathbf{x}_0= \frac{\mathbf{x}_t - \sqrt{1-\bar\alpha_t} \cdot \epsilon}{\sqrt{\bar \alpha_t}} \]
那既然如此,公式中 \(\bar \alpha_t\) 是已知的,只需要用模型去预测 \(\epsilon\) 即可,从而就可以从任意 \(\mathbf{x}_t\) 一步去噪得到图像 \(\mathbf{x}_0\) 。然而,需要思考的是, DDPM 本身其实是在学习真实图像的分布,再在这个分布采样得出真实图像,而真实图像分布是极其复杂的,因此一步采样就需要模型能直接拟合出这个复杂分布,这是不现实的(DDPM 原文也说明了这么做效果会很差,图像很模糊)。因此,DDPM 就尝试使用多次简单的概率分布采样(正态分布)来取代一次复杂的概率分布采样(真实图像分布)。
DDPM 的 Reverse Process 过程将需要进行多次采样,即逐步从 \(\mathbf{x}_t\) 到 \(\mathbf{x}_{t-1}\)最后再到图像 \(\mathbf{x}_0\)。由于 Reverse Process 过程是 Forward Process 的逆过程,那么我们可以尝试从 \(q(\mathbf{x}_{t}|\mathbf{x}_{t-1})=\mathcal{N}(\sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})\) 推导出 \(q(\mathbf{x}_{t-1}|\mathbf{x}_{t})\)。根据贝叶斯公式 \(P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}\) 可以得到:
\[ q(\mathbf{x}_{t-1}|\mathbf{x}_t) = \frac{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})\cdot q(\mathbf{x}_{t-1})}{q(\mathbf{x}_{t})} \]
然而, \(q(\mathbf{x}_{t-1}|\mathbf{x}_{t})\) 是无法直接被求解的,我们需要用整个数据集来估计这个概率分布,因此在 DDPM 中提出训练一个含参模型 \(p_\theta\) 来近似 \(q(\mathbf{x}_{t-1}|\mathbf{x}_{t})\) ,如下式其将逆过程 \(q(\mathbf{x}_{t-1}|\mathbf{x}_{t})\) 视为一个简单的正态分布,然后使用模型去预测这个分布的均值和方差(实际上没有,详情见下文分析)即可。
\[ p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right) \]
当我们已知 \(\mathbf{x}_0\) 的条件下,这个时候 \(q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_0)\) 是可以求解的,我们可以表示为:
\[ q(\mathbf{x}_{t-1}|\mathbf{x}_t,\mathbf{x}_0) = \frac{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})\cdot q(\mathbf{x}_{t-1}|\mathbf{x}_0)}{q(\mathbf{x}_{t}|\mathbf{x}_0)} \]
而我们已知 \(q(\mathbf{x}_{t}|\mathbf{x}_{t-1})=\mathcal{N}(\sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I})\) 和 \(q(\mathbf{x}_{t}|\mathbf{x}_{0})=\mathcal{N}(\sqrt{\bar \alpha_t} \mathbf{x}_{0}, ({1-\bar \alpha_t})\mathbf{I})\),再结合状态分布的概率分布函数 \(f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)\),可以直接将三个概率分布函数代入上式后得到:
\[ q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \sim \mathcal{N} \left( \frac{\sqrt{a_t}(1 - \bar{a}_{t-1})}{1 - \bar{a}_t} \mathbf{x}_t + \frac{\sqrt{\bar{a}_{t-1}}(1 - a_t)}{1 - \bar{a}_t} \mathbf{x}_0, \left( \frac{\sqrt{1 - a_t} \sqrt{1 - \bar{a}_{t-1}}}{\sqrt{1 - \bar{a}_t}} \right)^2 \right) \]
再代入\(\mathbf{x}_0= \frac{\mathbf{x}_t - \sqrt{1-\bar\alpha_t} \cdot \epsilon}{\sqrt{\bar \alpha_t}}\),即可得到和\(\mathbf{x}_0\)无关的表达式:
\[ q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \sim \mathcal{N} \left( \frac{\sqrt{{a}_t}(1 - \bar{a}_{t-1})}{1 - \bar{a}_t} \mathbf{x}_t + \frac{\sqrt{\bar{a}_{t-1}}(1 - a_t)}{1 - \bar{a}_t} \times \frac{\mathbf{x}_t - \sqrt{1 - \bar{a}_t} \times \epsilon}{\sqrt{\bar{a}_t}}, \left( \sqrt{\frac{\beta_t(1 - \bar{a}_{t-1})}{1 - \bar{a}_t}} \right)^2 \right) \]
进一步化简可得:
\[ q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \sim \mathcal{N}\left( \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon\right), \left( \sqrt{\frac{\beta_t(1 - \bar{a}_{t-1})}{1 - \bar{a}_t}} \right)^2 \right) \]
我们观察可以发现, \(p(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\) 的方差中不包括任何未知量,因此这部分无需估计,即 \(p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\) 中\(\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\)其实是一个无参量,需要预测的只有\(\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\):
\[ \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) = \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(\mathbf{x}_t,t)\right) \]
由于 \(\mathbf{x}_t\) 是已知的,可以发现我们这里需要预测的只是噪音 \(\epsilon_\theta(\mathbf{x}_t,t)\) ,所以只需要训练一个模型能预测 \(\epsilon_\theta(\mathbf{x}_t,t)\) 即可预测出 \(p_\theta\left(\mathbf{x}_{t-1} \mid \mathbf{x}_t\right)\),从而实现去噪。值得注意的是 \(\epsilon_\theta(\mathbf{x}_t,t)\) 近似的 \(\epsilon\) 其实是从 \(\mathbf{x}_0\) 到 \(\mathbf{x}_t\) 加入的噪音,而不是从 \(\mathbf{x}_{t-1}\) 到 \(\mathbf{x}_t\) 加入的噪音,因为这里的 \(\epsilon\) 来自于 \(\mathbf{x}_0= \frac{\mathbf{x}_t - \sqrt{1-\bar\alpha_t} \cdot \epsilon}{\sqrt{\bar \alpha_t}}\),最后可以通过 \(\epsilon\) 根据上式算出 \(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\) ,即可得到 \(\mathbf{x}_{t-1}\)。
按照常规的损失设计思路,既然是近似那直接用 MSE 损失,可以得出我们的训练损失为:
\[ L_t = \mathbb{E}_{t \sim [1,T], \mathbf{x}_0, \boldsymbol{\epsilon}} \left[ \left\| \boldsymbol{\epsilon} - \boldsymbol{\epsilon}_\theta (\mathbf{x}_t, t) \right\|^2 \right] \]
具体推导过程可参考 https://lilianweng.github.io/posts/2021-07-11-diffusion-models/ ,这里暂不作赘述。
文章作者 Littleor
上次更新 2024-09-08